Understanding Necessary and Sufficient condition

In this post, I will try to come up with examples from set theory as well as generic examples to help you understand necessity and sufficiency conditions better.

Case 1: A is both necessary and sufficient condition for B

Set Theory example: Two identical sets A & B.

• If an element belongs to B it implies it belongs to A (so A is necessary for B)
• and if an element belongs to A it implies it belongs to B. (so A is sufficient for B)

Generic Example:
“Being Red in colour is both necessary and sufficient condition for Tomatoes”

• This statement means that if something is tomato then it is red. If something is red then it is tomato.
• In other words, this statement is true if all tomatoes are red in colour and nothing else (other than tomatoes) is red in colour.

Symbolically: A ⇒ B B ⇒ A


Case 2: A is necessary but not sufficient condition for B

Set Theory example: B is subset of A.

• If an element belongs to B it implies that it belongs to A (so A is necessary for B)
• but if an element belongs to A it does not imply it belongs to B (so A is not sufficient for B)

Generic Example: “Being Red in colour is necessary but not sufficient condition for Tomatoes”

• This statement means that “if something is tomato then it is red, but if something is red then it need not be a tomato”
• In other words, this statement is true if all tomatoes are red in colour and things other than tomatoes are also red in colour.

Symbolically: B ⇒ A A ⇏ B


Case 3: Something is not necessary but sufficient condition for something else

Set Theory example: B is superset of A.

• If an element belongs to B it does not imply it belongs to A (so A is not necessary for B)
• but if an element belongs to A it implies that it also belongs to B. (so A is sufficient for B)

Generic Example: “Being red is not a necessary but it is a sufficient condition for Tomatoes”

• This statement means that if something is tomato then it need not be red, but if something is red then it must be a tomato
• In other words, this statement is true if only some tomatoes are red in colour (while some other tomatoes are green in colour etc) but nothing else (other than tomatoes) is red in colour.

Symbolically: B ⇏ A A ⇒ B


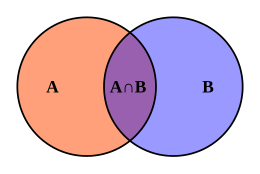
Case 4: Something is neither necessary nor sufficient condition for something else

Set Theory example: B is partially overlapping with A.

• If an element belongs to B it does not imply it belongs to A (so A is not necessary for B)
• and if an element belongs to A it does not imply it also belongs to B. (so A is not sufficient for B)

Generic Example: “Being red is neither necessary nor a sufficient condition for Tomatoes”

• This statement means that if something is tomato then it need not be red, and if something is red then it need not be a tomato
• In other words, this statement is true if only some tomatoes are red in colour (while some other tomatoes are green in colour etc) and things other than tomatoes are also red in colour.

Symbolically: A ⇏ B B ⇏ A